What Is a Family of Tests Simple Contrasts
Comparison Handling Groups with Linear Contrasts
Introduction
The omnibus \(F\)-exam appraises the evidence confronting the hypothesis of identical group means, just a rejection of this aught hypothesis provides piffling information well-nigh which groups differ and how. A very general and elegant framework for evaluating treatment grouping differences are linear contrasts, which provide a principled manner for amalgam corresponding \(t\)-tests and confidence intervals. In this affiliate, we develop this framework and employ information technology to our four drugs instance; we also consider several more complex examples to demonstrate its power and versatility.
If a set of contrasts is orthogonal, and then we can reconstitute the result of the \(F\)-exam using the results from the contrasts, and a significant \(F\)-examination implies that at least one dissimilarity is significant. If the \(F\)-test is not significant, we might still find significant contrasts, because the \(F\)-test considers all deviations from equal grouping ways simultaneously, while a dissimilarity looks for a specific ready of deviations for which it provides more than power past ignoring other potential deviations.
Because several contrasts leads to a multiplicity problem that requires adjusting conviction and significance levels. Several multiple comparing procedures allow the states to calculate these adjustments for different sets of contrasts.
Linear Contrasts
For our instance, nosotros might be interested in comparing the two drugs \(D1\) and \(D2\), for instance. One way of doing this is past a simple \(t\)-test between the corresponding observations. This yields a \(t\)-value of \(t=\) ii.22 and a \(p\)-value of \(p=\) 0.044 for a divergence of \(\chapeau{\mu}_1-\hat{\mu}_2=\) 1.52 with a 95%-confidence interval [0.05, 2.98]. While this approach yields a valid estimate and examination, information technology is inefficient because we completely fail the data available in the observations of drugs \(D3\) and \(D4\). Specifically, if nosotros presume that the variances are the same in all treatment groups, we could utilise these additional observations to go a improve estimate of the residual variance \(\sigma_e^2\) and increase the degrees of freedom.
We consider three example comparisons using our 4 drugs. Nosotros additionally assume that \(D1\) and \(D2\) share the same active component and denote these drugs every bit "Class A," while \(D3\) and \(D4\) share some other component ("Class B"):
- as before, compare the drugs in the first class: \(D1\) versus \(D2\);
- compare the drugs in the 2nd form: \(D3\) versus \(D4\);
- compare the classes: average of \(D1\) and \(D2\) versus average of \(D3\) and \(D4\).
We tin can formulate these comparisons in terms of differences of treatment grouping means; each is an instance of a linear contrast: \[\begin{align*} \text{D1 vs D2} &: \mu_1-\mu_2 \\ \text{D3 vs D4} &: \mu_3-\mu_4 \\ \text{Class A vs Class B} &: \left(\frac{\mu_1+\mu_2}{2}\right)-\left(\frac{\mu_3+\mu_4}{2}\right)\;. \end{align*}\] Note that a \(t\)-test for the third comparing requires transmission adding of the corresponding estimates and their standard errors first.
Linear contrasts use all information for estimation and 'automatically' pb to the correct \(t\)-test and confidence interval calculations. Their interpretation is one of the main purposes for an experiment:
Contrasts of interest justify the design, not the other way around.
An important task in designing an experiment is to ensure that contrasts of interest are defined beforehand and can be estimated with acceptable precision.
Defining Contrasts
Formally, a linear contrast \(\Psi(\mathbf{w})\) for a treatment factor with \(k\) levels is a linear combination of the group ways using a weight vector \(\mathbf{westward}=(w_1,\dots,w_k)\): \[ \Psi(\mathbf{westward}) = w_1\cdot\mu_1 + \cdots + w_k\cdot\mu_k \;, \] where the entries in the weight vector sum to zero, such that \(w_1+\cdots +w_k=0\).
Nosotros compare the group ways of two sets \(X\) and \(Y\) of handling cistron levels by selecting the weights \(w_i\) as follows:
- the weight of each handling level not considered is aught: \(w_i=0\iff i\not\in 10\) and \(i\not\in Y\);
- the weights for set \(X\) are all positive: \(w_i>0\iff i\in X\);
- the weights for set \(Y\) are all negative: \(w_i<0\iff i\in Y\);
- the weights sum to nothing: \(w_1+\cdots +w_k=0\);
- the individual weights \(w_i\) determine how the grouping ways of the sets \(X\) and \(Y\) are averaged; using equal weights with each ready corresponds to a simple average of the set's grouping ways.
The weight vectors for our example contrasts are \(\mathbf{w}_1=(+one,-1,0,0)\) for the first contrast, where \(10=\{one\}\) and \(Y=\{two\}\); \(\mathbf{w}_2=(0,0,+ane,-1)\) for the second, \(X=\{3\}\) and \(Y=\{4\}\); and \(\mathbf{w}_3=(+1/2, +one/two, -1/two, -i/2)\) for the tertiary contrast, where \(Ten=\{i,2\}\) and \(Y=\{iii,4\}\).
Estimating Contrasts
We judge a contrast by replacing the group means past their estimates: \[ \lid{\Psi}(\mathbf{w}) = w_1\cdot\hat{\mu}_1 + \cdots + w_k\cdot\hat{\mu}_k \;. \] Unbalancedness merely affects the precision simply not the interpretation of contrast estimates, and nosotros tin brand our exposition more than general by assuasive different numbers of samples per group, denoting by \(n_i\) the number of samples in group \(i\). From the properties of the group mean estimates \(\hat{\mu}_i\), we know that \(\hat{\Psi}(\mathbf{w})\) is an unbiased reckoner of the contrast \(\Psi(\mathbf{w})\) and has variance \[ \text{Var}\left(\lid{\Psi}(\mathbf{west})\right) = \text{Var}\left(w_1\cdot\lid{\mu}_1 + \cdots + w_k\cdot\lid{\mu}_k\correct) = \sum_{i=1}^k w_i^two \cdot\text{Var}(\chapeau{\mu}_i) = \sigma_e^two\cdot\sum_{i=1}^k \frac{w_i^2}{n_i}\;. \] We tin thus estimate its standard error by \[ \widehat{\text{se}}\left(\chapeau{\Psi}(\mathbf{w})\correct) = \hat{\sigma}_e\cdot\sqrt{\sum_{i=one}^chiliad\frac{w_i^2}{n_i}}\;. \] Note that the precision of a contrast estimate depends on the sizes for the involved groups (i.e., those with \(w_i\non= 0\)) in an unbalanced design, and standard errors are college for contrasts involving groups with low numbers of replicates in this case.
The estimate of a contrast is based on the ordinarily distributed estimates of the grouping means. We can use the remainder variance guess from the preceding ANOVA, and the resulting calculator for any dissimilarity has a \(t\)-distribution with all \(N-k\) degrees of freedom.
This immediately yields a \((i-\alpha)\)-conviction interval for a dissimilarity estimate \(\hat{\Psi}(\mathbf{due west})\): \[ \hat{\Psi}(\mathbf{westward}) \pm t_{\alpha/2, North-yard}\cdot \widehat{\text{se}}\left(\lid{\Psi}(\mathbf{w})\correct) = \chapeau{\Psi}(\mathbf{due west}) \pm t_{\alpha/ii, N-k}\cdot\hat{\sigma}_e\cdot\sqrt{\sum_{i=1}^k\frac{w_i^2}{n_i}}\;, \] where again \(t_{\blastoff/ii, N-yard}\) is the \(\alpha/two\)-quantile of the \(t\)-distribution with \(N-k\) degrees of freedom (\(N\) the total number of samples). If the degrees of freedom are sufficiently large, we can alternatively calculate the conviction interval based on the normal quantiles by replacing the quantile \(t_{\alpha/ii, Due north-m}\) with \(z_{\alpha/2}\).
For our third example contrast, we notice an estimate of \(\chapeau{\Psi}(\mathbf{w}_3)=\) four.28 for the difference between the average enzyme levels for a class A and class B drug. We already have an estimate \(\hat{\sigma}_e=\) 1.22 of the balance standard deviation: information technology is the root of the residual mean squares. The standard fault of \(\chapeau{\Psi}(\mathbf{w}_3)\) is given by \[ \widehat{\text{se}}(\chapeau{\Psi}(\mathbf{w}_3)) = \hat{\sigma}_e\cdot\sqrt{\left(\frac{(0.5)^2}{8}+\frac{(0.5)^2}{8}+\frac{(-0.5)^ii}{8}+\frac{(-0.5)^ii}{viii}\correct)}\approx 0.35\cdot\hat{\sigma}_e\;, \] which yields an estimated standard error of \(\widehat{\text{se}}(\chapeau{\Psi}(\mathbf{due west}_3))=\,\) 0.43.
From this, we calculate a \(t\)-based 95%-conviction interval of [iii.4, 5.sixteen], based on the \(t\)-quantile \(t_{0.025,28}=\) \(-ii.05\) for \(Due north-1000=\) 28 degrees of freedom. The conviction interval simply contains positive values and nosotros can therefore conclude that drugs in grade A have indeed a higher enzyme level than those in class B and the observed difference betwixt the classes is not likely due to random fluctuations in the data.
| Comparison | Contrast | Estimate | LCL | UCL |
|---|---|---|---|---|
| \(D1\)-vs-\(D2\) | \(\Psi(\mathbf{w}_1)=\mu_1-\mu_2\) | ane.51 | 0.27 | ii.76 |
| \(D3\)-vs-\(D4\) | \(\Psi(\mathbf{w}_2)=\mu_3-\mu_4\) | \(-0.1\) | \(-1.34\) | ane.15 |
| Class A-vs-Class B | \(\Psi(\mathbf{west}_3)=\frac{\mu_1+\mu_2}{two}-\frac{\mu_3+\mu_4}{two}\) | iv.28 | 3.4 | 5.16 |
Equivalent calculations for the remaining ii example contrasts \(\Psi(\mathbf{w}_1)\) and \(\Psi(\mathbf{w}_2)\) yield the estimates and 95%-confidence intervals in Tabular array v.1. The results suggest that the two drugs \(D1\) and \(D2\) in class A lead to unlike enzyme levels, if just slightly so. Annotation that the estimate for this dissimilarity is identical to our \(t\)-test issue, but the confidence interval is essentially narrower; this is the result of pooling the data for estimating the residual variance and increasing the degrees of liberty. The ii drugs in grade B cannot be distinguished based on the data.
Testing Contrasts
A linear dissimilarity estimate has a \(t\)-distribution for normally distributed response values. This allows us to derive a \(t\)-test for testing the zero hypothesis \[ H_0: \Psi(\mathbf{w}) = 0 \] using the test statistic \[ T = \frac{\lid{\Psi}(\mathbf{w})}{\widehat{\text{se}}(\hat{\Psi}(\mathbf{due west}))} = \frac{\sum_{i=1}^k w_i\lid{\mu}_i}{\lid{\sigma}_e\cdot \sqrt{\sum_{i=i}^kw_i^two/n_i}}\;, \] which has a \(t\)-distribution with \(Northward-thousand\) degrees of freedom if \(H_0\) is true.
For our 2nd example contrast, the \(t\)-statistic is \[ T = \frac{(0)\cdot \chapeau{\mu}_1 + (0)\cdot \lid{\mu}_2 + (+one)\cdot\chapeau{\mu}_3\,+\,(-i)\cdot\hat{\mu}_4}{\chapeau{\sigma}_e\cdot \sqrt{\frac{(0)^2+(0^two)+(+1)^ii+(-i)^ii}{8}}} = \frac{\hat{\mu}_3-\hat{\mu}_4}{\sqrt{2}\hat{\sigma}_e/\sqrt{8}}\;. \] This is exactly the statistic for a ii-sample \(t\)-test, but uses a pooled variance guess over all handling groups and \(N-k=\) 28 degrees of freedom. For our information, nosotros calculate \(t=\) \(-0.16\) and \(p=\) 0.88; the enzyme levels for drugs \(D3\) and \(D4\) cannot be distinguished. Equivalent calculations for all three case contrasts are summarized in Table five.2. Note again that for our first contrast, the \(t\)-value is near 10% larger than with the \(t\)-test based on the two groups alone, and the corresponding \(p\)-value is about one-half.
| Dissimilarity | Examination | \(t\) value | se | \(P(>|t|)\) |
|---|---|---|---|---|
| \(D1\)-vs-\(D2\) | \(H_0: \mu_1-\mu_2=0\) | ii.49 | 0.61 | 1.89e-02 |
| \(D3\)-vs-\(D4\) | \(H_0:\mu_3-\mu_4=0\) | \(-0.16\) | 0.61 | 8.75e-01 |
| Class A-vs-Grade B | \(H_0:\frac{\mu_1+\mu_2}{2}-\frac{\mu_3+\mu_4}{2}=0\) | 9.96 | 0.43 | i.04e-10 |
Using Contrasts in R
The emmeans package provides for the heavy lifting: nosotros calculate the analysis of variance using aov(), estimate the group means using emmeans(), and define a list of contrasts which we estimate using contrast().
Nosotros are usually more interested in conviction intervals for contrast estimates than we are in \(t\)-values and test results. Conveniently, the confint() function takes a contrast() result directly and by default yields 95%-confidence intervals for our contrasts.
For our three example contrasts, the post-obit code performs all required calculations in just v commands:
one thousand = aov(y~drug, data=drugs) em = emmeans(g, ~drug) ourContrasts = listing( "D1-vs-D2" = c(1,- 1,0,0), "D3-vs-D4" = c(0,0,one,- 1), "Form A-vs-Course B" = c(1 / 2,ane / 2,- 1 / 2,- 1 / two) ) estimatedContrasts = contrast(em, method=ourContrasts) ci = confint(estimatedContrasts) Orthogonal Contrasts and ANOVA Decomposition
At that place is no limit on the number of contrasts that we might gauge for any prepare of data. On the other hand, contrasts are linear combinations of the \(one thousand\) group ways and we likewise demand to guess the thousand mean.2 That means that we can find exactly \(k-one\) contrasts that exhaust the information available in the group means and whatever additional contrast can be calculated from results of these \(1000-1\) contrasts. This idea is made formal by saying that two contrasts \(\Psi(\mathbf{w})\) and \(\Psi(\mathbf{v})\) are orthogonal if \[ \sum_{i=ane}^k \frac{w_i\cdot v_i}{n_i} = 0\;. \] This requirement reduces to the more interpretable 'usual' orthogonality condition \(\sum_i w_i\cdot v_i = 0\) for a balanced design.
Our three example contrasts are all pairwise orthogonal; for example, we have \(\sum_i w_{1,i}\cdot w_{2,i}=(+1\cdot 0)+(-1\cdot 0)+(0\cdot +one)+(0\cdot -ane)=0\) for the first and second contrast. With \(k=4\), simply three contrasts can be mutually orthogonal and our three contrasts thus fully frazzle the available information.
If 2 contrasts \(\Psi(\mathbf{w})\) and \(\Psi(\mathbf{v})\) are orthogonal, then the associated null hypotheses \[ H_0: \Psi(\mathbf{due west})=0 \quad \text{and} \quad H_0: \Psi(\mathbf{five})=0 \] are logically independent in the sense that nosotros tin can larn aught about one being true or fake by knowing the other existence true or false.three
A set up of \(k-1\) orthogonal contrasts decomposes the treatment sum of squares into \(k-i\) contrast sums of squares. The sum of squares of a contrast \(\Psi(\mathbf{w})\) is \[ \text{SS}_{\mathbf{w}} = \frac{\left(\sum_{i=1}^k w_i\hat{\mu}_i\right)^two}{\sum_{i=ane}^kw_i^ii/n_i}\;, \] and each dissimilarity has one degree of freedom: \(\text{df}_{\mathbf{w}}=1\). We can use the \(F\)-statistic \[ F = \frac{\text{SS}_{\mathbf{w}}/1}{\chapeau{\sigma}_e^2} = \frac{\text{SS}_{\mathbf{w}}}{\text{MS}_\text{res}} \] with 1 numerator and \(North-g\) denominator degrees of liberty for testing \(H_0: \Psi(\mathbf{w})=0\); this is equivalent to the \(t\)-test.
For our case contrasts, we detect \(\text{SS}_{\mathbf{due west}_1}=\) 9.eighteen, \(\text{SS}_{\mathbf{west}_2}=\) 0.04, and \(\text{SS}_{\mathbf{w}_3}=\) 146.68 with associated \(F\)-values \(F_{\mathbf{w}_1}=\) six.21, \(F_{\mathbf{w}_2}=\) 0.03, and \(F_{\mathbf{w}_3}=\) 99.27, each with 1 numerator and 28 denominator degrees of freedom. Annotation that \(\sqrt{F_{\mathbf{west}_1}}=\) 2.49 corresponds precisely to the absolute value of the previous \(t\)-statistic in Table five.ii, for example.
We can reconstitute the motorbus \(F\)-test for the treatment factor from the dissimilarity \(F\)-tests. In particular, we know that if the bus \(F\)-test is significant, and then is at least i of the contrasts in an orthogonal set up. For our example, we observe the handling sum of squares equally \(\text{SS}_{\mathbf{w}_1}+\text{SS}_{\mathbf{due west}_2}+\text{SS}_{\mathbf{west}_3}=\) 155.89, and the handling \(F\)-value as \((F_{\mathbf{w}_1}+F_{\mathbf{westward}_2}+F_{\mathbf{westward}_3})/three=\) 35.17. These results correspond exactly to the values from our previous ANOVA (Tab. 4.2).
Orthogonal contrasts provide a systematic way to ensure that the information of an experiment are fully wearied in the analysis. In exercise, scientific questions are sometimes more directly addressed by sets of non-orthogonal contrasts which are and so preferred for their easier interpretation, even though their hypothesis tests might be logically dependent and contain redundancies.
Contrasts for Ordered Factors
The order of levels of Drug is completely arbitrary: we could just as well put the drugs of Form B equally the first two levels and those of Grade A as levels 3 and four. For some treatment factors, levels are ordered and level \(i\) is 'smaller' than level \(i+1\) in some well-defined sense; such factors are called ordinal. For example, our treatment might consist of our current drug \(D1\) administered at every bit spaced concentrations \(C_0<C_1<C_2<C_3<C_4\). Data for 8 mice per concentration are shown in Effigy 5.ane and indicate that the drug'southward effect is negligible for the first two or iii concentrations, then increases substantially and seems to decrease once again for higher concentrations.
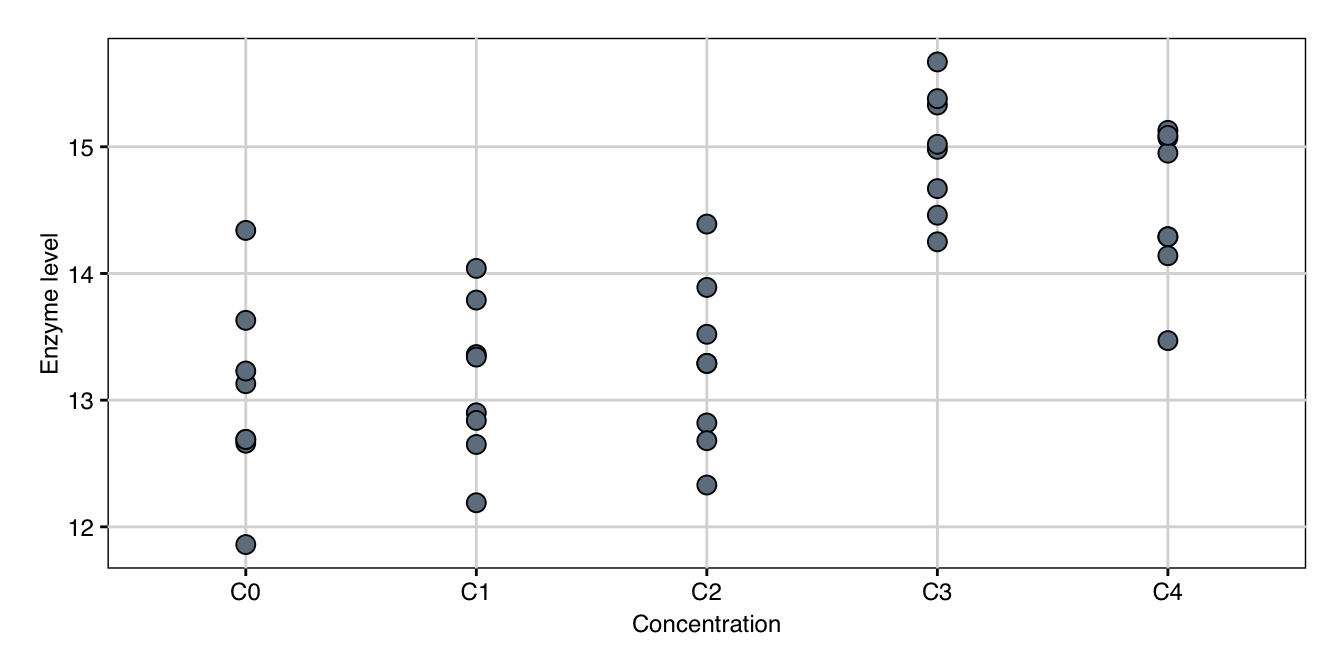
Effigy five.1: Enzyme levels for v increasing concentrations of drug D1.
Trend Assay using Orthogonal Polynomials
We can analyze such information using ordinary contrasts, but with ordered treatment gene levels, it makes sense to look for trends. We exercise this using orthogonal polynomials, which are linear, quadratic, cubic, and quartic polynomials that decompose a potential trend into different components. Orthogonal polynomials are formulated as a special set of orthogonal contrasts. Nosotros utilize the emmeans() and contrast() combination again, and ask for a poly contrast to generate the advisable set of orthogonal contrasts:
m.conc = aov(y~concentration, data=drug_concentrations) em.conc = emmeans(m.conc, ~concentration) ct.conc = contrast(em.conc, method= "poly") The contrast weight vectors for our case are shown in Tabular array v.3.
| Linear | Quadratic | Cubic | Quartic | |
|---|---|---|---|---|
| C0 | -2 | 2 | -ane | 1 |
| C1 | -1 | -1 | ii | -4 |
| C2 | 0 | -2 | 0 | half dozen |
| C3 | 1 | -one | -2 | -4 |
| C4 | 2 | 2 | 1 | i |
Each polynomial contrast measures the similarity of the shape of the data to the design described by the weight vector. The linear polynomial measures an upward or down tendency, while the quadratic polynomial measures curvature in the response to the concentrations, such that the trend is non only a proportional increase or decrease in enzyme level. Cubic and quartic polynomials measure more complex curvature, but become harder to interpret direct.
| Contrast | Approximate | se | df | t value | P(>|t|) |
|---|---|---|---|---|---|
| linear | four.88 | 0.70 | 35 | half-dozen.95 | four.38e-08 |
| quadratic | 0.50 | 0.83 | 35 | 0.61 | 5.48e-01 |
| cubic | -2.14 | 0.lxx | 35 | -3.05 | four.40e-03 |
| quartic | -5.20 | ane.86 | 35 | -two.80 | viii.32e-03 |
For our data, we get the result in Table 5.4. We find a highly meaning positive linear trend, which means that on boilerplate, the enzyme level increases with increasing concentration. The negligible quadratic together with significant cubic and quartic trend components means that in that location is curvature in the data, but it is irresolute with the concentration. This reflects the fact that the data prove a large increase for the fourth concentration, which then levels off or decreases at the fifth concentration, leading to a sigmoidal pattern.
Time Trends
Some other typical example for an ordered gene is time. Nosotros have to be careful about the experimental blueprint, however. For example, measuring the enzyme levels at four timepoints using unlike mice per timepoint can be analyzed using orthogonal polynomials and an analysis of variance arroyo. This is because each mouse can be randomly allocated to one timepoint, yielding a completely randomized blueprint. If, however, the design is such that the same mice are measured at 4 different timepoints, then the assumption of random assignment is violated and analysis of variance with contrasts is no longer a reasonable analysis option.4 This type of longitudinal design, where the same unit is followed over time, requires more specialized methods to capture the inherent correlation between timepoints. We briefly hash out simple longitudinal designs in Section 8.four.
Minimal Constructive Dose
Another example of contrasts useful for ordered factors are the orthogonal Helmert contrasts. They compare the second level to the kickoff, the 3rd level to the average of the first and second level, the fourth level to the average of the preceding three, and so forth.
Helmert contrasts can be used for finding a minimal effective dose in a dose-response study. Since doses are typically in increasing order, we first exam the second-lowest against the lowest dose. If the corresponding average responses cannot exist distinguished, we presume that no effect of relevant size is present (provided the experiment is not underpowered). We then pool the information of these two doses and use their common average to compare against the third-smallest dose, thereby increasing the precision compared to contrasting each level just to its preceding level.
Helmert contrasts are not straight available in emmeans, but the package manual tells us how to define them ourselves:
helmert.emmc = role(ordered.levels, ...) { # Use built-in R contrast to find dissimilarity matrix contrast.matrix = as.data.frame(contr.helmert(ordered.levels)) # Provide useful name for each contrast names(contrast.matrix) = paste(ordered.levels[- one],"vs lower") # Provide name of dissimilarity gear up attr(dissimilarity.matrix, "desc") = "Helmert contrasts" return(contrast.matrix) } In our example data in Effigy v.i, the concentration \(C_3\) shows a clear result. The situation is much less clear-cut for lower concentrations \(C_0,\dots, C_2\); in that location might be a hint of linear increase, just this might be due to random fluctuations. Using the Helmert contrasts
ct.helmert = contrast(em.conc, "helmert") yields the contrasts in Table 5.5 and the results in Table v.6. Concentrations \(C_0, C_1, C_2\) evidence no discernible differences, while enzyme levels increase significantly for concentration \(C_3\), indicating that the minimal effective dose is between concentrations \(C_2\) and \(C_3\).
| Concentration | C1 vs lower | C2 vs lower | C3 vs lower | C4 vs lower |
|---|---|---|---|---|
| C0 | -1 | -i | -i | -1 |
| C1 | 1 | -ane | -1 | -1 |
| C2 | 0 | two | -i | -one |
| C3 | 0 | 0 | 3 | -i |
| C4 | 0 | 0 | 0 | 4 |
| Contrast | Estimate | se | df | t value | P(>|t|) |
|---|---|---|---|---|---|
| C1 vs lower | 0.11 | 0.31 | 35 | 0.35 | vii.28e-01 |
| C2 vs lower | 0.38 | 0.54 | 35 | 0.71 | 4.84e-01 |
| C3 vs lower | 5.47 | 0.77 | 35 | vii.xi | 2.77e-08 |
| C4 vs lower | 3.fourscore | 0.99 | 35 | 3.83 | five.10e-04 |
Standardized Effect Size
Similar to our previous discussions for unproblematic differences and motorbus \(F\)-tests, we might sometimes turn a profit from a standardized effect size measure for a linear dissimilarity \(\Psi(\mathbf{w})\), which provides the size of the contrast in units of standard difference.
A first idea is to directly generalize Cohen'due south \(d\) every bit \(\Psi(\mathbf{westward})/\sigma_e\) and measure out the contrast estimate in units of the standard departure. A trouble with this approach is that the measure nonetheless depends on the weight vector: if \(\mathbf{w}=(w_1,\dots,w_k)\) is the weight vector of a dissimilarity, then we can ascertain an equivalent contrast using, for example, \(\mathbf{westward}'=ii\cdot\mathbf{due west}=(2\cdot w_1,\dots,2\cdot w_k)\). Then, \(\Psi(\mathbf{west}')=2\cdot\Psi(\mathbf{westward})\), and the above standardized measure also scales appropriately. In addition, we would like our standardized issue measure to equal Cohen'due south \(d\) if the contrast describes a uncomplicated deviation between ii groups.
Both issues are resolved past Abelson'south standardized issue size measure \(d_\mathbf{w}\) (Abelson and Prentice 1997): \[ d_\mathbf{w} = \sqrt{\frac{2}{\sum_{i=1}^one thousand w_i^2}}\cdot \frac{\Psi(\mathbf{w})}{\sigma_e} \;\text{estimated by}\; \hat{d}_\mathbf{w}=\sqrt{\frac{2}{\sum_{i=1}^k w_i^ii}}\cdot \frac{\hat{\Psi}(\mathbf{w})}{\hat{\sigma}_e}\;. \]
For our scaled dissimilarity \(\mathbf{w}'\), we discover \(d_\mathbf{w'}=d_\mathbf{due west}\) and the standardized effect sizes for \(\mathbf{w}'\) and \(\mathbf{west}\) coincide. For a simple difference \(\mu_i-\mu_j\), we accept \(w_i=+i\) and \(w_j=-1\), all other weights being nothing. Thus \(\sum_{i=ane}^k w_i^2=2\) and \(d_\mathbf{w}\) is reduced to Cohen'due south \(d\).
Power Analysis and Sample Size
The power calculations for linear contrasts can be done based on the contrast estimate and its standard mistake, which requires calculating the power from the noncentral \(t\)-distribution. We follow the equivalent approach based on the contrast'southward sum of squares and the residual variance, which requires calculating the power from the noncentral \(F\)-distribution.
Verbal Method
The noncentrality parameter \(\lambda\) of the \(F\)-distribution for a contrast is given equally \[ \lambda = \frac{\Psi(\mathbf{w})^2}{\text{Var}(\hat{\Psi}(\mathbf{w}))} = \frac{\left(\sum_{i=1}^one thousand w_i\cdot \mu_i\correct)^2}{\frac{\sigma^2}{n}\sum_{i=1}^k w_i^2} = n\cdot 2\cdot \left(\frac{d_\mathbf{w}}{ii}\correct)^ii = n\cdot 2\cdot f^2_\mathbf{w}\;. \] Notation that the final term has exactly the same \(\lambda=northward\cdot k\cdot f^2\) class that nosotros encountered previously, since a contrast uses \(k=2\) (sets of) groups and we know that \(f^2=d^2/4\) for direct group comparisons.
From the noncentrality parameter, we tin can summate the ability for testing the null hypothesis \(H_0: \Psi(\mathbf{w})=0\) for any given significance level \(\alpha\), residual variance \(\sigma_e^2\), sample size \(n\), and causeless real value of the contrast \(\Psi_0\), respectively the assumed standardized effect size \(d_{\mathbf{w},0}\). Nosotros calculate the power using our getPowerF() function and increment \(north\) until nosotros reach the desired power.
For our first example contrast \(\mu_1-\mu_2\), nosotros notice \(\sum_i w_i^2=two\). For a minimal difference of \(\Psi_0=\) 2 and using a residual variance estimate \(\hat{\sigma}_e^2=\) 1.five, nosotros calculate a noncentrality parameter of \(\lambda=\) 1.33 \(n\). The numerator degree of freedom is df1=1 and the denominator degrees of freedom are df2=n*4-4. For a significance level of \(\alpha=5\%\) and a desired power of \(1-\beta=80\%\), we discover a required sample size of \(north=\) 7. We arrive at a very conservative gauge by replacing the residual variance by the upper confidence limit \(\text{UCL}=\) ii.74 of its estimate. This increases the required sample size to \(n=\) 12. The sample size increases substantially to \(n=\) 95 if nosotros want to detect a much smaller contrast value of \(\Psi_0=0.5\).
Similarly, our third example contrast \((\mu_1+\mu_2)/ii - (\mu_3+\mu_4)/2\) has \(\sum_i w_i^2=1\). A minimal value of \(\Psi_0=2\) can be detected with 80% ability at a v% significance level for a sample size of \(due north=\) 4 per group, with an verbal power of 85% (for \(n=\) 3 the power is 70%). Even though the desired minimal value is identical to the get-go example contrast, we demand less samples since we are comparing the average of ii groups to the boilerplate of ii other groups, making the judge of the difference more precise.
The overall experiment size is so the maximum sample size required for any dissimilarity of interest.
Portable Power
For making the power analysis for linear contrasts portable, we apply the same ideas every bit for the double-decker \(F\)-exam. The numerator degrees of freedom for a contrast \(F\)-test is \(\text{df}_\text{num}=one\) and we detect a sample size formula of \[ north = \frac{2\cdot\phi^2\cdot\sigma_e^two\cdot\sum_{i=one}^k w_i^2}{\Psi_0^ii} = \frac{\phi^2}{(d_\mathbf{due west}/2)^two} = \frac{\phi^two}{f_\mathbf{due west}^2}\;. \] For a unproblematic difference contrast, \(\sum_i w_i^2=ii\), we accept \(\Psi_0=\delta_0\). With the approximation \(\phi^2\approx 4\) for a power of 80% at a 5% significance level and \(grand=2\) cistron levels, we derive our old formula again: \(north=16/(\Psi_0/\sigma_e)^two\).
For our showtime example contrast with \(\Psi_0=ii\), we detect an approximate sample size of \(n\approx\) half dozen based on \(\phi^2=3\), in reasonable agreement with the verbal sample size of \(n=\) 7. If we instead ask for a minimal difference of \(\Psi_0=0.5\), this number increases to \(n\approx\) 98 mice per drug handling group (exact: \(n=\) 95).
The sample size is lower for a contrast between two averages of group means. For our third case contrast with weights \(\mathbf{w}=(1/2, 1/ii, -1/2, -i/ii)\) we find \(due north=viii/(\Psi_0/\sigma_e)^2\). With \(\Psi_0=2\), this gives an approximate sample size of \(n\approx\) five (exact: iv).
Multiple Comparisons and Mail-Hoc Analyses
Introduction
Planned and Post-Hoc Contrasts
The employ of orthogonal contrasts—pre-defined before the experiment is conducted—provides no further difficulty in the assay. They are, however, oft inconvenient for an informative analysis: we may want to use more than \(k-1\) planned contrasts every bit part of our pre-defined analysis strategy. In addition, exploratory experiments lead to post-hoc contrasts that are based on observed outcomes. Post-hoc contrasts likewise play a office in advisedly planned and executed confirmatory experiments, when peculiar patterns emerge that were not anticipated, simply require further investigation.
We must carefully distinguish between planned and post-hoc contrasts: the first case just points to the limitations of independent pre-divers contrasts, but the contrasts and hypotheses are nonetheless pre-defined at the planning stage of the experiment and before the data is in. In the second case, we 'scarlet-pick' interesting results from the data after the experiment is washed and we inspected the results. This course of action increases our gamble of finding false positives. A common example of a post-hoc contrast occurs when looking at all pair-wise comparisons of treatments and defining the deviation between the largest and smallest group mean as a contrast of involvement. Since there is always one pair with greatest departure, it is incorrect to use a standard \(t\)-test for this contrast. Rather, the resulting \(p\)-value needs to be adapted for the fact that we ruby-picked our dissimilarity, making it larger on boilerplate than the dissimilarity of whatever randomly chosen pair. Properly adjusted tests for post-hoc contrasts thus take lower ability than those of pre-defined planned contrasts.
The Problem of Multiple Comparisons
Whether we are testing several pre-planned contrasts or post-hoc contrasts of some kind, we also have to adjust our analysis for multiple comparisons.
Imagine a scenario where we are testing \(q\) hypotheses, from \(q\) contrasts, say. We want to control the false positive probability using a significance level of \(\alpha\) for each individual test. The probability that any individual exam falsely rejects the naught hypothesis of a zero deviation is then \(\alpha\). Nonetheless, fifty-fifty if all \(q\) null hypotheses are true, the probability that at to the lowest degree one of the tests will incorrectly turn down its null hypothesis is not \(\alpha\), but rather \(1-(ane-\alpha)^q\).
For \(q=200\) contrasts and a significance level of \(\blastoff=5\%\), for example, the probability of at least ane incorrect rejection is 99.9965%, a well-nigh certainty.v Indeed, the expected number of false positives, given that all 200 null hypotheses are true, is \(200\cdot \alpha=10\). Even if we only test \(q=5\) hypotheses, the probability of at to the lowest degree one incorrect rejection is 22.6% and thus substantially larger than the desired false positive probability.
The probability of at least 1 false positive in a family unit of tests (the family-wise or experiment-wise error probability) increases with the number of tests, and in any case exceeds the private exam's significance level \(\blastoff\). This is known every bit the multiple testing problem. In essence, we have to make up one's mind which error we want to control: is information technology the private error per hypothesis or is it the overall mistake of at to the lowest degree one wrong announcement of significance in the whole family of hypotheses?
A multiple comparison process (MCP) is an algorithm that computes adjusted significance levels for each individual test, such that the overall mistake probability is bound by a pre-divers probability threshold. Some of the procedures are universally applicable, while others a predicated on specific classes of contrasts (such as comparing all pairs), merely offer higher power than more full general procedures. Specifically, (i) the universal Bonferroni and Bonferroni-Holm corrections provide control for all scenarios of pre-defined hypotheses; (ii) Tukey's honest significant departure (HSD) provides control for testing all pairs of groups; (3) Dunnett's method covers the case of comparing each grouping to a common control grouping; and (4) Scheffé'south method gives conviction intervals and tests for any mail service-hoc comparisons suggested by the data.
These methods apply mostly for multiple hypotheses. Here, nosotros focus on testing \(q\) contrasts \(\Psi(\mathbf{w}_l)\) with \(q\) null hypotheses \[ H_{0,l}: \Psi(\mathbf{westward}_l)=0 \] where \(\mathbf{w}_l=(w_{1l},\dots,w_{kl})\) is the weight vector describing the \(50\)th contrast.
Full general Purpose: Bonferroni-Holm
The Bonferroni and Holm corrections are popular and unproblematic methods for decision-making the family unit-wise fault probability. Both work for arbitrary sets of planned contrasts, merely are conservative and atomic number 82 to depression significance levels for the individual tests, often much lower than necessary.
The uncomplicated Bonferroni method is a single-step process to control the family-wise fault probability by adjusting the individual significance level from \(\alpha\) to \(\alpha/q\). Information technology does not consider the observed information and rejects the nada hypothesis \(H_0: \Psi(\mathbf{w}_l)=0\) if the contrast exceeds the critical value based on the adjusted \(t\)-quantile: \[ \left|\lid{\Psi}(\mathbf{w}_l)\right| > t_{1-\alpha/2q, N-1000}\cdot\chapeau{\sigma}_e\cdot \sqrt{\sum_{i=one}^grand\frac{w_{il}^2}{n_i}}\;. \] It is easily practical to existing test results: simply multiply the original \(p\)-values by the number of tests \(q\) and declare a test pregnant if this adjusted \(p\)-value stays below the original significance level \(\alpha\).
For our three example contrasts, we previously establish unadjusted \(p\)-values of \(0.019\) for the first, \(0.875\) for the 2d, and \(10^{-10}\) for the 3rd contrast. The Bonferroni adjustment consists of multiplying each by \(q=iii\), resulting in adjusted \(p\)-values of \(0.057\) for the first, \(2.626\) for the second (which we cap at \(1.0\)), and \(3\times 10^{-ten}\) for the tertiary contrast, moving the starting time contrast from significant to not significant at the \(\blastoff=5\%\) level. The resulting contrast estimates and \(t\)-test are shown in Table 5.7.
| Contrast | Estimate | se | df | t value | P(>|t|) |
|---|---|---|---|---|---|
| D1-vs-D2 | 1.51 | 0.61 | 28 | 2.49 | 5.66e-02 |
| D3-vs-D4 | -0.x | 0.61 | 28 | -0.16 | 1.00e+00 |
| Class A-vs-Class B | 4.28 | 0.43 | 28 | 9.96 | three.13e-ten |
The Bonferroni-Holm method is based on the same assumptions, but uses a multi-footstep procedure to find an optimal significance level based on the observed information. This increases its power compared to the simple procedure. Permit us telephone call the unadjusted \(p\)-values of the \(q\) hypotheses \(p_1,\dots,p_q\). The method first sorts the observed \(p\)-value such that \(p_{(1)}<p_{(2)}<\cdots <p_{(q)}\) and \(p_{(i)}\) is the \(i\)th smallest observed \(p\)-value. It then compares \(p_{(ane)}\) to \(\alpha/q\), \(p_{(ii)}\) to \(\blastoff/(q-ane)\), \(p_{(iii)}\) to \(\alpha/(q-ii)\) and and then on until a \(p\)-value exceeds its corresponding threshold. This yields the smallest alphabetize \(j\) such that \[ p_{(j)} > \frac{\alpha}{q+one-j}\;, \] and whatsoever hypothesis \(H_{0,i}\) for which \(p_i<p_{(j)}\) is declared significant.
Comparisons of All Pairs: Tukey
We gain more ability if the set of contrasts has more construction and Tukey's method is designed for the mutual instance of all pairwise differences. It considers the distribution of the studentized range, the difference betwixt the maximal and minimal group ways past calculating honest pregnant differences (HSD) (Tukey 1949a). It requires a balanced pattern and rejects \(H_{0,l}: \Psi(\mathbf{west}_l) = 0\) if \[ \left|\hat{\Psi}(\mathbf{west}_l)\correct| > q_{one-\blastoff,one thousand-one,N}\cdot\hat{\sigma}_e\cdot \sqrt{\frac{ane}{ii}\sum_{i=one}^k\frac{w_{il}^2}{n}} \quad\text{that is}\quad |\hat{\mu}_i-\chapeau{\mu}_j| > q_{one-\alpha,chiliad-ane,N}\cdot\frac{\hat{\sigma}_e}{\sqrt{n}}\;, \] where \(q_{\alpha,chiliad-one,Due north}\) is the \(\blastoff\)-quantile of the studentized range based on \(grand\) groups and \(Due north=n\cdot k\) samples.
The upshot is shown in Table 5.8 for our example. Since the departure between the ii drug classes is very large, all but the two comparisons within each form yield highly pregnant estimates, but neither difference of drugs in the aforementioned course is significant after Tukey'due south aligning.
Comparisons Against a Reference: Dunnett
Another very common blazon of biological experiment uses a control group and inference focuses on comparing each treatment with this command group, leading to \(1000-i\) contrasts. These contrasts are not orthogonal, and the required aligning is provided by Dunnett's method (Dunnett 1955). It rejects the null hypothesis \(H_{0,i}: \mu_i-\mu_1=0\) that treatment group \(i\) shows no deviation to the control group 1 if \[ |\chapeau{\mu}_i-\hat{\mu}_1| > d_{i-\alpha, yard-1, Due north-k}\cdot\chapeau{\sigma}_e\cdot\sqrt{\frac{1}{n_i}+\frac{1}{n_1}}\;, \] where \(d_{one-\alpha, one thousand-1, Northward-k}\) is the quantile of the appropriate distribution for this test.
For our example, let us presume that drug \(D1\) is the all-time current treatment selection, and we are interested in comparing the alternatives \(D2\) to \(D4\) to this reference. The required contrasts are the differences from each drug to the reference \(D1\), resulting in Table v.eight.
| Contrast | Guess | se | df | t value | P(>|t|) |
|---|---|---|---|---|---|
| Pairwise-Tukey | |||||
| D1 - D2 | one.51 | 0.61 | 28 | 2.49 | 8.30e-02 |
| D1 - D3 | 5.09 | 0.61 | 28 | 8.37 | two.44e-08 |
| D1 - D4 | iv.99 | 0.61 | 28 | 8.21 | iii.59e-08 |
| D2 - D3 | 3.57 | 0.61 | 28 | 5.88 | i.45e-05 |
| D2 - D4 | three.48 | 0.61 | 28 | 5.72 | 2.22e-05 |
| D3 - D4 | -0.10 | 0.61 | 28 | -0.sixteen | 9.99e-01 |
| Reference-Dunnett | |||||
| D2 - D1 | -one.51 | 0.61 | 28 | -two.49 | v.05e-02 |
| D3 - D1 | -5.09 | 0.61 | 28 | -viii.37 | 1.24e-08 |
| D4 - D1 | -4.99 | 0.61 | 28 | -8.21 | 1.82e-08 |
Unsurprisingly, enzyme levels for drug \(D2\) are barely distinguishable from those of the reference drug \(D1\), and \(D3\) and \(D4\) testify very different responses than the reference.
General Purpose and Post-Hoc Contrasts: Scheffé
The method by Scheffé is suitable for testing whatever group of contrasts, even if they were suggested by the data (Scheffé 1959); in contrast, most other methods are restricted to pre-defined contrasts. Naturally, this liberty of cherry-picking comes at a price: the Scheffé method is extremely bourgeois (so furnishings take to exist huge to be deemed meaning), and is therefore only used if no other method is applicative.
The Scheffé method rejects the null hypothesis \(H_{0,l}\) if \[ \left|\hat{\Psi}(\mathbf{w}_l)\right| > \sqrt{(thou-1) \cdot F_{\blastoff,k-1,N-k}} \cdot \lid{\sigma}_e \cdot \sqrt{\sum_{i=1}^k \frac{w_{il}^2}{n_i}}\;. \] This is very similar to the Bonferroni correction, except that the number of contrasts \(q\) is irrelevant, and the quantile is a scaled quantile of an \(F\)-distribution rather than a quantile from a \(t\)-distribution.
For illustration, imagine that our three case contrasts were non planned before the experiment, but rather suggested by the information after the experiment was completed. The adjusted results are shown in Table v.9.
| Contrast | Estimate | se | df | t value | P(>|t|) |
|---|---|---|---|---|---|
| D1-vs-D2 | 1.51 | 0.61 | 28 | 2.49 | 1.27e-01 |
| D3-vs-D4 | -0.10 | 0.61 | 28 | -0.16 | 9.99e-01 |
| Class A-vs-Class B | four.28 | 0.43 | 28 | 9.96 | 2.40e-09 |
Nosotros notice that the \(p\)-values are much more conservative than with any other method, which reflects the added dubiety due to the post-hoc nature of the contrasts.
A Real-Life Example—Drug Metabolization
Nosotros further illustrate the ane-manner ANOVA and apply of linear contrasts using a existent-life instance (Lohasz et al. 2020).6 The two anticancer drugs cyclophosphamide (CP) and ifosfamide (IFF) become active in the human body only after metabolization in the liver past the enzyme CYP3A4, among others. The part of this enzyme is inhibited by the drug ritanovir (RTV), which more than strongly affects metabolization of IFF than CP. The experimental setup consisted of 18 independent channels distributed over several microfluidic devices; each aqueduct contained a co-civilisation of multi-cellular liver spheroids for metabolization and tumor spheroids for measuring drug action.
The experiment used the diameter of the tumor (in \(\mu\text{m}\)) subsequently 12 days as the response variable. There are six treatment groups: a control condition without drugs, a 2d status with RTV solitary, and the four conditions CP only, IFF only, and the combined CP:RTV and IFF:RTV. The resulting information are shown in Figure 5.2A for each channel.
A preliminary analysis revealed that device-to-device variation and variation from channel to aqueduct were negligible compared to the inside-aqueduct variance, and these two factors were consequently ignored in the analysis. Thus, data are pooled over the channels for each treatment group and the experiment is analyzed as a (slightly unbalanced) 1-style ANOVA. We discuss an alternative ii-way ANOVA in Section vi.three.8.
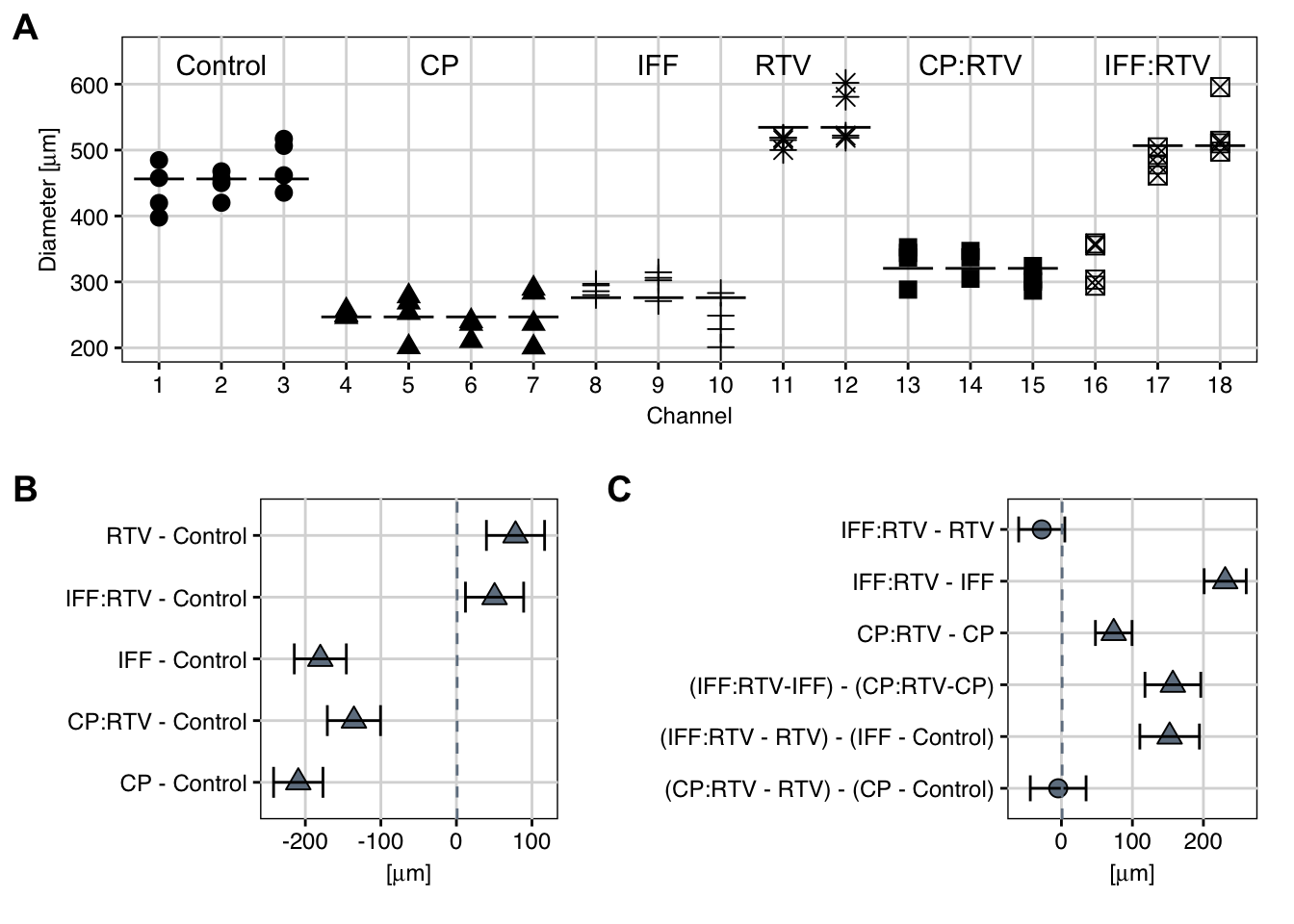
Effigy 5.two: A: Observed diameters by channel. Bespeak shape indicates handling. Aqueduct 16 appears to be mislabelled. B: Estimated treatment-versus-control contrasts and Dunnett-adjusted 95%-confidence intervals based on data excluding channel 16, meaning contrasts are indicated as triangles. C: Equally (B) for specific (unadjusted) contrasts of interest.
Inhomogeneous Variances
The omnibus \(F\)-test and linear contrast assay crave equal within-group variances between treatment groups. This hypothesis was tested using the Levene examination and a \(p\)-value below 0.5% indicated that variances might differ substantially. If true, this would complicate the analysis. Looking at the raw data in Effigy 5.2A, however, reveals a potential error in aqueduct 16, which was labelled as IFF:RTV, but shows tumor diameters in fantabulous understanding with the neighboring CP:RTV handling. Including channel 16 in the IFF:RTV group then inflates the variance estimate. It was therefore decided to remove channel 16 from further assay, the hypothesis of equal variances is then no longer rejected (\(p>0.ix\)), and visual inspection of the data confirms that dispersions are very similar between channels and groups.
Assay of Variance
As is expected from looking at the data in Figure v.2A, the i-way analysis of variance of tumor bore versus treatment results in a highly pregnant treatment effect.
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Condition | five | 815204.ix | 163040.98 | 154.53 | 6.34e-33 |
| Residuals | sixty | 63303.4 | 1055.06 |
The effect sizes are an explained variation of \(\eta^ii=\) 93%, a standardized effect size of \(f^2=\) 12.88, and a raw effect size of \(b^2=\) 13589.one\(\mu\text{thousand}^2\) (an average departure between group ways and full general mean of \(b=\) 116.57\(\mu\text{m}\))
Linear Contrasts
Since the \(F\)-test does not elucidate which groups differ and by how much, nosotros continue with a more than targeted assay using linear contrasts to estimate and test meaningful and interpretable comparisons. With a first set of standard contrasts, we compare each treatment group to the control condition. The resulting dissimilarity estimates are shown in Figure 5.2B together with their Dunnett-corrected 95%-confidence intervals.
Somewhat surprisingly, the RTV-only condition shows tumor diameters significantly larger than those under the control condition, indicating that RTV alone influences the tumor growth. Both conditions involving CP evidence reduced tumor diameters, indicating that CP inhibits tumor growth, as does IFF alone. Lastly, RTV seems to substantially decrease the efficacy of IFF, leading again to tumor diameters larger than under the control condition, but (at least visually) comparable to the RTV condition.
The big and pregnant difference between command and RTV-only poses a trouble for the interpretation: we are interested in comparing CP:RTV against CP-only and similarly for IFF. But CP:RTV could be a combined effect of tumor diameter reduction by CP (compared to command) and increment by RTV (compared to control). We have two options for defining a meaningful contrast: (i) estimate the difference in tumor diameter between CP:RTV and CP. This is a comparing between the combined and single drug actions. Or (two) estimate the divergence betwixt the alter in tumor bore from CP to control and the alter from CP:RTV to RTV (rather than to control). This is a comparison between the baseline tumor diameters under control and RTV to those under addition of CP and is the net-result of CP (provided that RTV increases tumor diameters equally with and without CP).
The ii sets of comparisons atomic number 82 to different contrasts, but both are meaningful for these information. The authors of the study decided to go for the first type of comparison and compared tumor diameters for each drug with and without inhibitor. The 2 contrasts are \(\text{IFF:RTV}-\text{IFF}\) and \(\text{CP:RTV}-\text{CP}\), shown in rows 2 and three of Figure 5.2C. Both contrasts show a large and significant increase in tumor diameter in the presence of the inhibitor RTV, where the larger loss of efficacy for IFF yields a more pronounced difference.
For a complete estimation, we are too interested in comparing the two differences between the CP and the IFF weather: is the reduction in tumor diameter under CP smaller or larger than nether IFF? This question addresses a difference of differences, a very common type of comparison in biological science, when different conditions are contrasted and a 'baseline' or control is bachelor for each condition. Nosotros express this question equally \((\text{IFF:RTV}-\text{IFF}) - (\text{CP:RTV}-\text{CP})\), and nosotros can sort the terms to derive the contrast form \((\text{IFF:RTV}+\text{CP}) - (\text{CP:RTV}+\text{IFF})\). Thus, nosotros apply weights of \(+1\) for the treatment groups IFF:RTV and CP, and weights of \(-1\) for the groups CP:RTV and IFF to define the contrast. Annotation that this differs from our previous instance dissimilarity comparing drug classes, where nosotros compared averages of several groups by using weights \(\pm 1/2\). The estimated contrast and confidence interval is shown in the fourth row in Figure five.2C: the two increases in tumor diameter nether co-administered RTV are significantly unlike, with about 150 \(\mu\text{g}\) more under IFF than under CP.
For comparison, the remaining two rows in Figure 5.2C show the tumor diameter increase for each drug with and without inhibitor, where the no-inhibitor condition is compared to the control condition, merely the inhibitor condition is compared to the RTV-only condition. Now, IFF shows less increase in tumor diameter than in the previous comparison, but the event is withal big and significant. In contrast, nosotros do not find a difference between the CP and CP:RTV conditions indicating that loss of efficacy for CP is simply marginal under RTV. This is because the previously observed difference can be explained by the difference in 'baseline' betwixt control and RTV-only. The contrasts are constructed equally before: for CP, the comparison is \((\text{CP:RTV}-\text{RTV}) - (\text{CP}-\text{Control})\) which is equivalent to \((\text{CP:RTV}+\text{Control}) - (\text{RTV} + \text{CP})\).
Conclusion
What started equally a seemingly straightforward one-way ANOVA turned into a much more intricate assay. Only the straight inspection of the raw information revealed the source of the heterogeneous treatment group variances. The untestable assumption of a mislabelling followed by removal of the data from aqueduct xvi still led to a straightforward autobus \(F\)-test and ANOVA table.
Great care is too required in the more detailed contrast analysis. While the RTV-only condition was initially thought to provide some other command status, a comparing with the empty control revealed a systematic and substantial difference, with RTV-just showing larger tumor diameters. Two sets of contrasts are and then plausible, using different 'baseline' values for estimating the effect of RTV in conjunction with a drug. Both sets of contrasts have straightforward interpretations, but which prepare is more meaningful depends on the biological question. Notation that the of import contrast of tumor diameter differences betwixt inhibited and uninhibited weather condition compared between the ii drugs is independent of this decision.
Notes and Summary
Using R
Interpretation of contrasts in R is discussed in Section 5.2.4. A very user-friendly option for applying multiple comparisons procedures is to use the emmeans package and follow the same strategy as before: guess the model parameters using aov() and estimate the group means using emmeans(). We can then utilize the contrast() function with an adapt= argument to choose a multiple correction process to conform \(p\)-values and conviction intervals of contrasts. This role also has several frequently used sets of contrasts built-in, such as method="pairwise" for generating all pairwise contrasts or method="trt.vs.ctrl1" and method="trt.vs.ctrlk" for generating contrasts comparing all treatments to the showtime, respectively last, level of the treatment factor. For estimated marginal ways em, and either the corresponding built-in contrasts or our manually divers set up of contrasts ourContrasts, nosotros admission the v procedures as
dissimilarity(em, method=ourContrasts, adapt= "bonferroni") contrast(em, method=ourContrasts, adjust= "holm") contrast(em, method= "pairwise", adjust= "tukey") contrast(em, method= "trt.vs.ctrl1", conform= "dunnett") contrast(em, method=ourContrasts, arrange= "scheffe") By default, these functions provide the contrast estimates and associated \(t\)-tests. We tin can use the results of contrast() as an input to confint() to get contrast estimates and their adapted conviction intervals instead.
The package Superpower provides functionality to perform power analysis of contrasts in conjunction with emmeans.
Summary
Linear contrasts are a principled way for defining comparisons between two sets of group ways and constructing the respective estimators, their confidence intervals, and \(t\)-statistics. While an ANOVA passenger vehicle \(F\)-examination looks for any pattern of divergence between group means, linear contrasts use specific comparisons and are more powerful in detecting the specified deviations. Without much exaggeration, linear contrasts are the primary reason for conducting comparative experiments and their definition is an important part of an experimental design.
With more than than one hypothesis tested, multiple comparison procedures are oftentimes required to suit for the inflation in faux positives. Full general purpose procedures are easy to utilise, but sets of contrasts often have more structure that can be exploited to proceeds more power.
Power analysis for contrasts poses no new bug, but the adjustments past MCPs can simply be considered for single-step procedures, because multi-step procedures depend on the observed \(p\)-values which are of course unknown at the time of planning the experiment.
Source: https://n.ethz.ch/~kahans/doe2021/ch-contrastsmcp.html
0 Response to "What Is a Family of Tests Simple Contrasts"
Postar um comentário